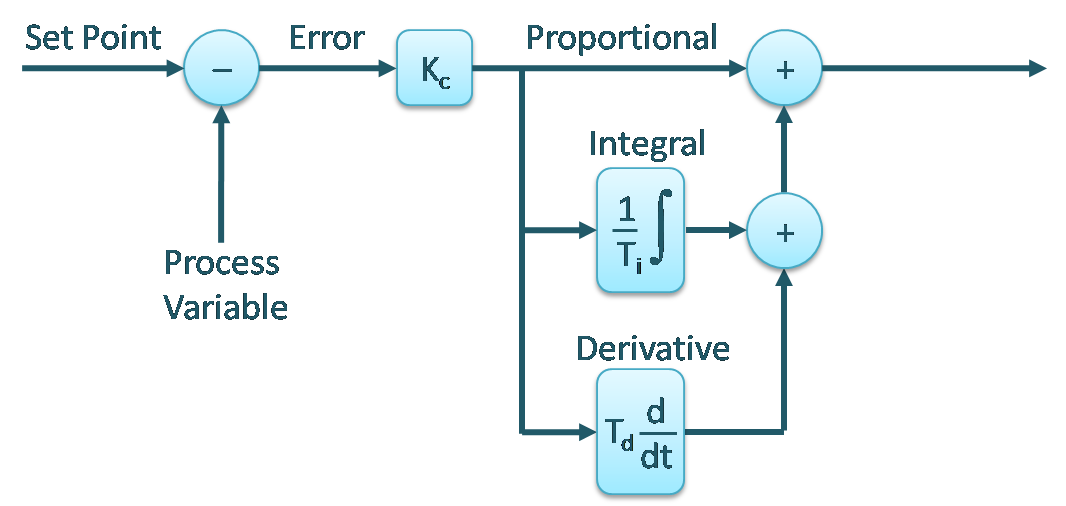
The Proportional Derivative Integrative Control

What is a controller? What does a controller do? These questions need to be answered before diving into the types and uses of different controllers. We have a system and like every system it has a purpose. Every system there are input signals and the result of these input signals are output signals. The whole purpose of controllers is to figure out the appropriate input signals to extract the required output signals. In simplest of words, find the right input to get the desired output. Whenever we talk about control systems, the feedback control system comes to mind. For any system we want to get a specific output. The job of the controller is to get the required output based on the input. When this resulting output is fed back and compared to the desired output, an error is calculated. What we want in our controller is to at least try to minimize and in some cases, nullify this error so that there is no discrepancy between the desired output and the actual output.

For example, I want to walk ten meters ahead. In this case I am the system, my current actual output is zero meters( because I haven’t started) and my desired output is ten meters. In this instance my error is ten minus zero meters which is ten. Now my controller, which is my brain will use this error to generate the necessary input signal to input into the actuator which in this case, are my legs and I walk. My current actual output is constantly changing and is being fed back to calculate the error, hence the name feedback. This calculation of error and actuation will continue until I reach my target destination and the error becomes zero. This is what I want my controller ( my brain) to achieve. What does this all have to do with the PID controller? The P in PID stands for proportional term. This term or gain is multiplied with the error term. In the example of walking ten meters, If the error at any instance is ten meters and my brain has a proportional gain of 0.1, my brain would command my legs to walk at the speed of one meter per second. So eventually as I near my target destination the speed at which I approach the destination keeps on decreasing because for the error of five meters, the speed will be 0.1 times five equals 0.5. Hence, the target destination will be reached asymptotically as the error will be driven to zero. The controller with only the proportional gain is called P controller.

It is clear from the example cited above that this proportional term has the ability to achieve what is desired. So, why are the I and the D term required? Let’s look at an example of a drone. The process is the same: the drone is initially in the ground and the required position of the drone is ten meters, but this distance to cover is the altitude. Like before our proportional term, will be multiplied with the error ( which in this case is the difference between required altitude and the current actual altitude) and the necessary output signal based on this is calculated. The difference is, in this case once the drone reaches the desired altitude the error will become zero making the input command zero too. So, when the drone reaches the altitude of ten meters, the drone’s actuators or the motors will stop and the drone will start to fall down. When this happens there will be an error which the proportional term again multiply and generate the necessary actuating signal. At some proportional gain the actuating signal ( in this case the motor speed) and the weight of the drone will nullify each other resulting in the drone hovering in an altitude lower than the desired altitude. The altitude the drone will hover will depend upon the drone’s weight and the proportional gain. The gain could be increased as much as we can to decrease the error and achieve the desired altitude but there will always be an error which will not be nullified, proving proportional gain is not sufficient.

This ever present error which cannot be nullified is called steady state error. Like in the example of the drone where the drone is stable and steady but the error is present. This steady state error must be dealt with to completely cancel the error to achieve the desired result , in our case the desired altitude. This is where the I term or the integrative gain comes into play. By using this gain we are making use of the past information. The integrative term like its name integrates the error meaning the error from the past is kept on added and fed to the controller. The question is how does this help in nullifying the steady state error. Going back to our drone example, when the drone becomes stable and there is a small ever present error. This small error will be insignificant to the proportional term but when added on for several time stamps this error will become significant forcing the controller to act. Let’s say the drone reaches an altitude of nine meters and becomes stable. Let’s say the steady state error is one meters. This error is very small for proportional gain to make it significant, but if this error of one meter resides for five seconds and the error is being calculated once every second, the integrated error after five seconds will become five meters, making this error significant and forcing the controller to react. This way by adding an integrative gain the PI controller will be able to cancel the steady state error. Now the million dollar question is what do we need the D term for?

Once again consider our example of a drone. The proportional term becomes significant to minimize the major error and the integrative term will aid in the steady state term. However, the integrative term is active even before the drone reaches stability. So as the drone is increasing its altitude the integrated error will accumulate to a large error further speeding the motors, this will result in the drone surpassing the desired altitude resulting in negative error ( If the drone reaches twelve meters, the desired altitude minus the current actual altitude becomes negative two meters). This phenomenon is called overshoot. This overshoot is not desirable and to prevent this we need something to take into account how fast the error is decreasing or changing. This is where the D term or the derivative gain comes into action. The derivative gain is the result of the differentiation of the error. This gives us information about the rate of change of error. By taking the rate of change of error into account, necessary signals can be generated ahead of time to prevent the overshooting. For example, if our drone is rapidly approaching the desired altitude of ten meters suggesting a high rate of change of error. The derivative term will induce a reaction from the controller to prevent the controller from generating a signal that will result in negative error making the system more stable. This way when the three terms( Proportional , Derivative , Integrative ) are added and work together, this controller is called the PID controller.