The State Observation
The Kalman filter is an optimal estimation algorithm. Now this seems very underwhelming. To understand this, let’s dive straight into an example. Let’s say I have to measure the temperature of the fire inside a furnace. How do I measure it? It’s simple right? Just stick a sensor and read. Unfortunately, it's not that simple. The sensor or the material used in the sensor will most likely melt itself or get destroyed failing to measure the internal temperature. Now how do we solve this problem? We can measure the external temperature of the furnace. The question is how does measuring external temperature do us any good in this case? The answer is by using the external temperature , we can make an estimation of the internal temperature. The kalman filter is an algorithm which enables us to make optimal estimations of the state of any system.
To measure the position of our car, the data from IMU , odometer and the satellite are used. The data from all these sources are prone to drift and disturbances. To make them reliable and more accurate, Kalman filters can be used to estimate the car’s position based on the data from these three sources. Some common applications of Kalman Filter are guidance and navigation systems, computer vision and signal processing. One of the first uses of Kalman Filters was in the Apollo Project. It was used to predict the trajectory of the spacecraft.
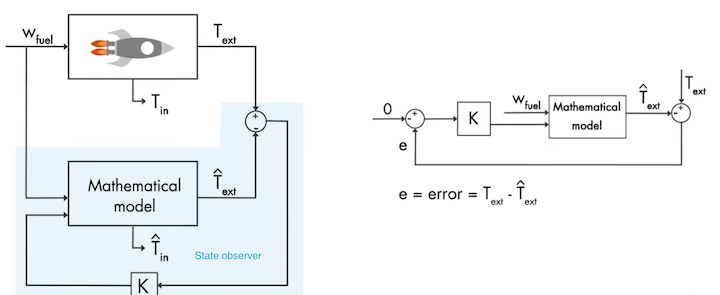
To get a deeper understanding of the topic, we need to understand state observation. State observation is the process of estimating something that cannot be seen or measured directly. For example, we want to measure the internal temperature of the rocket exhaust to calculate the fuel flow. But the problem is directly measuring the internal temperature of the exhaust is not possible. However, there is a way to measure the external temperature. Can we measure the internal temperature using the available information about the fuel flow and the external temperature? We can’t. But we do have a mathematical model of the system or the rocket’s exhaust. By using the value of the fuel flow rate we might be able to mathematically calculate the ideal external temperature and internal temperature at that rate ( focus on the word ideal). So, the problem is solved right? Wrong. You see the mathematical model is the ideal representation of the system and the actual system will have many uncertainties and disturbances. This is the reason why we need a state estimator to measure the real state of the system which in our case is the real internal temperature.
Let’s see how all this works in our example of rocket exhaust. We will try to match the estimated external temperature with the real external temperature. We are doing this in order to converge the mathematical model which is ideal to the best approximation of the real system. Let’s say the real internal and external temperature are t_i and t_o. Also assume that the estimated internal and external temperatures are T_i and T_o. What we are trying to achieve is to minimize T_o - t_o such that the difference between T_i and t_i also gets minimized meaning they become very close to each other. This all minimizing and comparing might sound similar to the control enthusiasts like myself and it is similar. Like in the feedback control where we try to minimize the error to the value of zero, we are trying to minimize the difference between the real internal temperature and the estimated internal temperature to zero. The idea is by using the fuel flow in the mathematical model, we find the ideal external temperature (T_o). We then calculate the error (T_o - t_o) and feed this error back through a gain K to drive this error to zero.