State Observer Mathematically

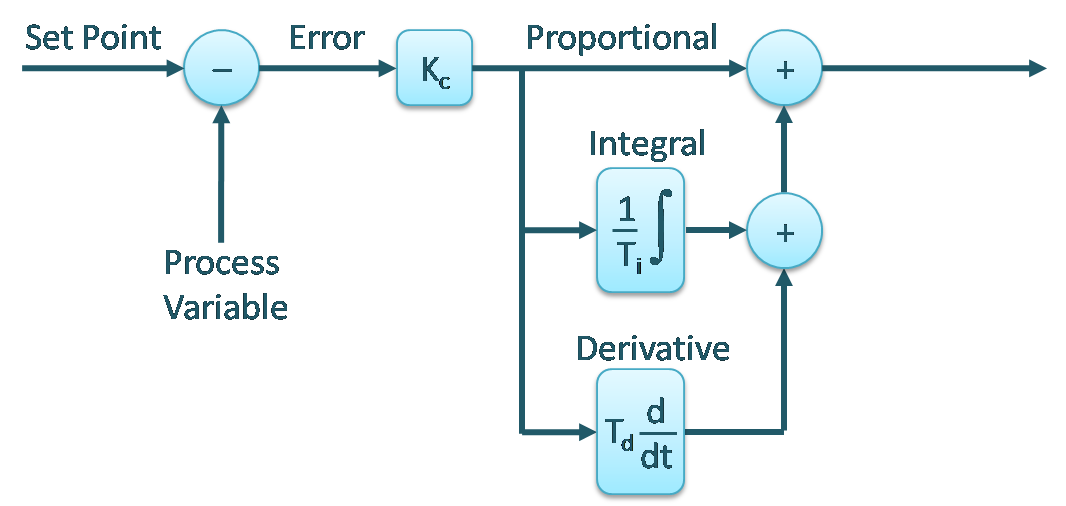
I have talked about the state observers basics in an earlier blog. The earlier introduction did not dive into mathematics but this article’s purpose is to do so. To get a feel of the problem at hand let’s refer once again to the figure below. To understand this figure and the basic content refer to the introductory article on the state observer.

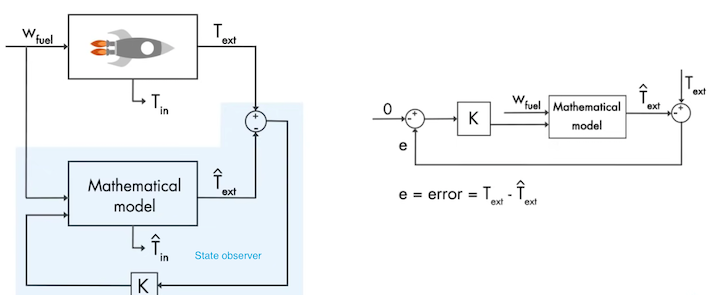
Firstly, let’s generalize the inputs and outputs as u and y. Let us also assume the state to be estimated as x. Let us also write the equations for the system and the mathematical model.

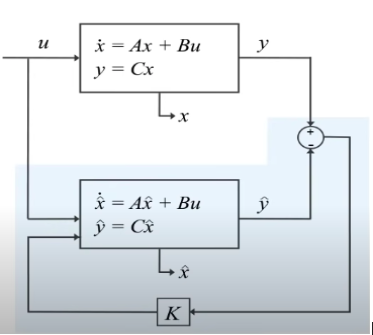
What we want to achieve from all this is to drive the predicted state to the actual state or x_hat to x. Let the difference between x_hat and x be an error defined as observer error or e_obs. If we write the equations for the actual system and the mathematical model and subtract one from the other we will get error dynamics. If we rearrange some terms, another set of equations can be derived. The figure below incorporates all the information talked about in this paragraph.

If we look more closely it is clear that the solution of the first equation of the rearranged error dynamics is an exponential function with an exponent of (A-KC)t.

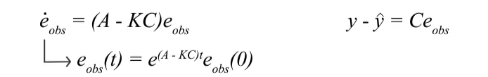
Now if the (A-KC) < 0 then e_obs will be near zero as the t nears infiniti resulting in x_hat nearing x. What this means is that, over time our error will vanish to zero and this will result in x_hat converging to x which is exactly what we want.

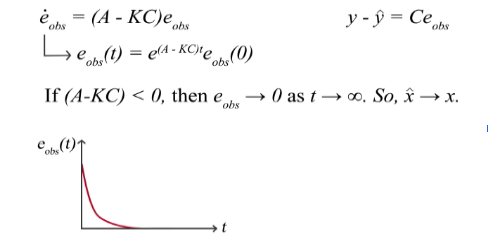
One question might be on the need of the KC term as it is clear that even without the KC term the error will still converge to zero. The significance of this is that by including this term or by including a feedback, we can control the rate of decay of the error by proper selection of the gain K. The optimal choice for this gain K can be done by using the Kalman Filters.